|
|
Corribus


Hero of Order
The Abyss Staring Back at You
|
 posted May 11, 2010 06:39 PM
posted May 11, 2010 06:39 PM |
|
|
@dimis
Thanks for the analysis of Risk. I'm wondering, as a pseudo-problem suitable for this thread: if you were tasked with improving the game by changing the rules, how would you do it?
|
|
friendofgunnar

    
     
Honorable
Legendary Hero
able to speed up time
|
 posted May 11, 2010 11:54 PM
posted May 11, 2010 11:54 PM |
|
|
Quote:
Anyway, let's come back to your initial question, which is about the "optimal configuration of troops" between two countries. First of all, you are also hiding additional information... But regardless, the natural way of rephrasing the "optimal splitting" of the army is to find the configuration that minimizes the probability that the attacker wins.
To simplify the problem you can say that it's just one army stack trying to conquer two of your regions, one after the other. The defender's goal is to stop the attacker from winning both territories - if the attacker only wins one territory then the defender has "won the war" so to speak. So the question is if it makes a difference how you distribute your forces amongst those two countries. I can give a hint and say the solution is the same for all situations where the attacker and defender have more than 3 armies.
I'll give the answer in a day or so to give anybody else time to guess.
Quote:
And here I will give you an anecdote... So, now the two other players wanted to punish us and both of them came after me.
It's true that faction making is a big part of the game. In online play I've found that teams crystallize and dissolve constantly. And then if they stab you in the back you get to leave a nasty note on their comment board 
Quote:
Do you want to know how the exact values are computed via Markov Chains in the second plot above ?
Actually yeah, I am still curious about how to solve this from a purely mathematical standpoint.
|
|
dimis

   
    
Responsible
Supreme Hero
Digitally signed by FoG
|
 posted May 12, 2010 09:22 PM
posted May 12, 2010 09:22 PM |
|
Edited by dimis at 02:15, 16 May 2010.
|
Ok, finally a well defined problem for which I don't know the end result, but I already described the approach. So, here is the approach that you asked. A/D represents the amount A of units of the attacker and D represents the amount D of units of the defender. I chose 10 as the maximum amount of units for the attacker, but this is arbitrary. We can use 30, 100, 1000, or whatever instead of 10.
Attacker <= 10 Units, Defender 1 Unit
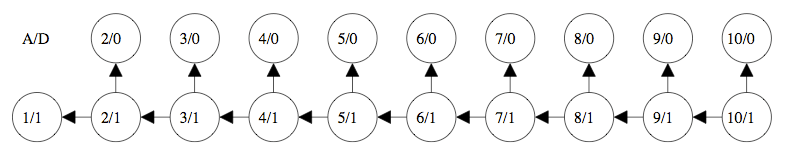
Care is needed so that we write down the right numbers on the arrows.
Now create two matrices R,Q with the rows and columns interpreted like below.
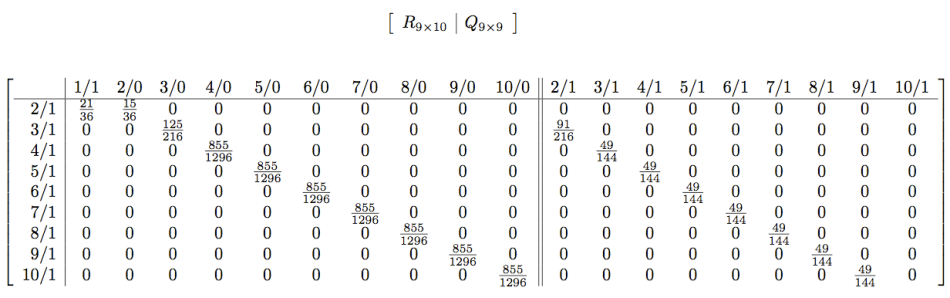
The entry (i,j) gives the transition probability from state i to state j.
Now we want the inverse
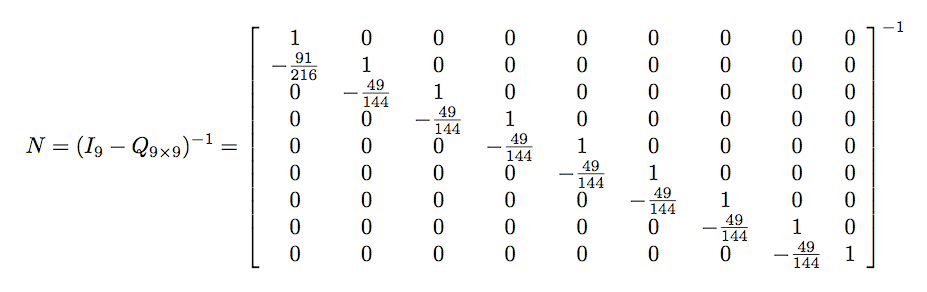
which is

Multiply the above matrix with R and we get
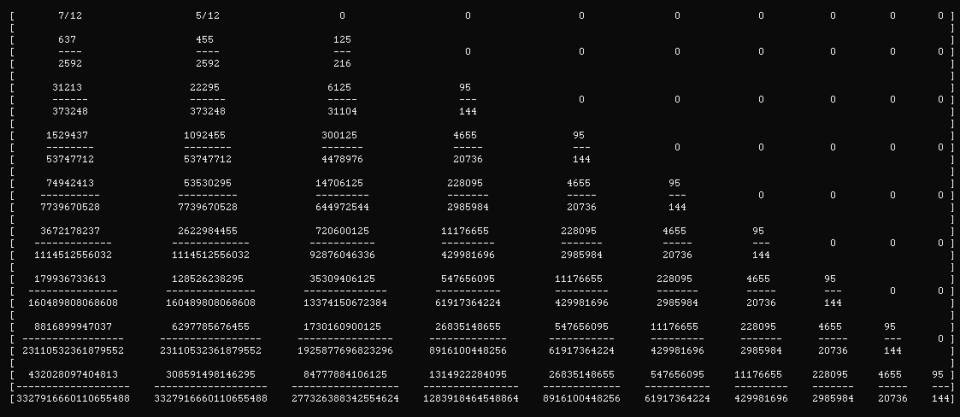
which is about
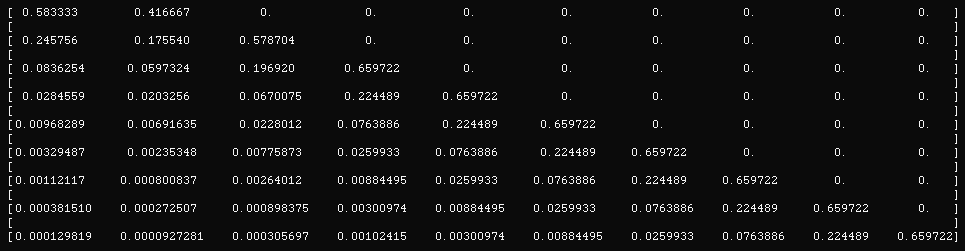
Each row of this last matrix from top to bottom is again interpreted as in the R matrix; so first row is 2/1, second row is 3/1, ..., last row is 10/1. Each column is every final state; from left to right it is 1/1, 2/0, 3/0, ..., 10/0.
Now pick any row in this matrix. The entries on that row give us the probabilities of reaching the state at the corresponding column in the end.
So, for example if the attacker starts with 10 units and the defender has 1 unit, in the end the attacker has 7 units with probability about 2.6%. Similarly if the attacker starts with 9 units, will end up with 6 units with probability about 2.6% again; which is the reasonable thing, given the setup and the rules of the game (the losses are the same and all dice rolls are the same). As a final example, when the attacker has 8 units, he will end up with 7 units with probability about 22.45%. And so on ... In particular, the first entry of the last row, the way the table is, gives us the probability that the attacker with 10 Units will lose 9 units when he is facing a defender with just 1 unit (and hence the attacker loses). The sum of all the other values in that row gives the probability that the attacker wins in general; regardless of how many units are left in the end. However, because of the fact that we split all "winning" situations of the attacker to the different cases of units left in the end, we also know now the entire distribution among all possible outcomes. If you want a different interpretation, the final row now gives us vertical cuts on the plot that we have earlier for A=10 at the vertical line D=1.
We do the same thing for D=2, to obtain the numbers there.
Attacker <= 10 Units, Defender 2 Units
The chain now is

Similar computations like above here. The order in which the columns come are
1/2,1/1,2/0,3/0,4/0,5/0,6/0,7/0,8/0,9/0,10/0,2/1,2/2,3/1,4/1,4/2,5/1,6/1,6/2,7/1,8/1,8/2,9/1,10/2. The blue part are the columns on the R matrix like above. The green part are the columns on the Q matrix like above; these are also the entries of the rows from top to bottom.
The end results (rounded) for this case are
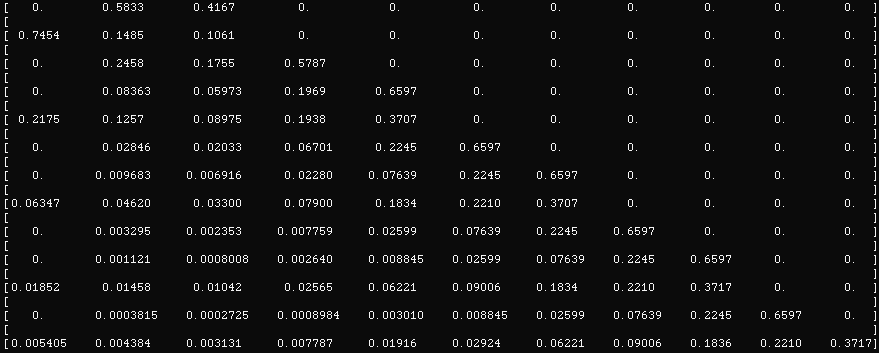
Can we justify the zeros in the first column ? What more can we say there ?
We repeat the process for all other cases of the defender, say up to 9 units (I am not willing to do it right now; we can come back to this one during the summer).
Once this is done, your question can be viewed as a 2-step process by forming pairs of the modules that we created above; essentially this is another chain. The idea is to contract each of the above diagrams, so that we remove the intermediate states, and leave present the starting state of each diagram as well as every possible final state. We now connect with arrows the starting state with all the final states in the new diagram, and the transition probabilities are given from the last row of the matrix that we have computed earlier. This is one module which gives in a compact way the result of the first battle. Every final state of this component is used as the starting point for another similar module (it denotes the starting army for the attacker), again based on the previous results. Made up from these 2 components we have the final chain that we are interested in for this particular defending configuration, where adding up all the "winning" entries in the last row of the matrix will give us the probability that the attacker wins this particular configuration of defending armies between the two countries. We repeat the process for all other possible defending pairs, every time computing in the end the probability that the attacker wins, and whichever value is minimum, suggests the optimal defending configuration for this particular setup; whatever this is.
____________
The empty set
|
|
friendofgunnar

    
     
Honorable
Legendary Hero
able to speed up time
|
 posted May 13, 2010 06:48 PM
posted May 13, 2010 06:48 PM |
|
|
I get it, piece of cake 

Solution:
If your goal is to prevent the capture of both territories the best way to divide your army is like this:
N-2 & 2
I'll give 12 armies as an example. The first number is the number of armies on average that it will take to conquer both territories. The two numbers in parenthesis is the way that you split your army.
11.87077 (10 2 )
11.82464 ( 6 6 )
11.8136 ( 8 4 )
11.78653 ( 7 5 )
11.74921 ( 9 3 )
11.68528 (11 1 )
As you can see, N-1 & 1 is the worst way to split your army. Here's another statistical output for 17 armies.
16.13216 (15 2 )
16.08927 (11 6 )
16.08452 (10 7 )
16.06947 ( 9 8 )
16.01959 (14 3 )
16.06457 (13 4 )
16.02982 (12 5 )
15.96964 (16 1 )
And six armies:
6.76546 ( 4 2 )
6.60521 ( 3 3 )
6.55634 ( 5 1 )
This couplet 'rule' applies to other circumstances also. If you are trying to prevent an enemy from completely chomping you, the more couplets you have the stronger you'll be.
For example your enemy has 15 armies. You have 8 armies and 4 territories. He has a 89.13% chance of eliminating you from the game if you place your armies like this: 5,1,1,1
but he only has an 83.66% chance of eliminating you if you spread your armies like this: 2,2,2,2
(BTW all numbers cited are derived statistically, not mathematically.)
Next risk problem:
One way to start the game is by placing 3 armies on every territory, with all the territories divided up amongst the players. On everybody's first turn they get 3 armies to place anywhere. The typical strategy is to put all 3 armies on one territory and try to conquer another territory so you can get a card. But what if you have two territories sitting next to the one that you're trying conquer? (another situation that's very typical). Is the typical strategy the best one?
So here's the setup. The first two numbers are your territories. The third is the opponent.
3 3 3
You place 3 armies. Should you put 3 on one and attack?
6 3 3
Or should you place 2 on the first and 1 on the second and attack?
5 4 3
You also have two different playing options:
A) Win at all costs (Keep attacking from the territory with the best odds and keep attacking even if the odds are against you. This means either you win or you have 1 and 1 armies left over)
B) Conserve your strength (keep attacking from the territory with the best odds and stop when the odds go against you).
For the complete solution you have to say what is the best placement under both playing styles.
I'm currently working on this mathematically (thankyou very much for the explanation Dimis). I'm not sure how long that'll take though...
|
|
dimis

   
    
Responsible
Supreme Hero
Digitally signed by FoG
|
 posted May 13, 2010 07:18 PM
posted May 13, 2010 07:18 PM |
|
|
Yeah, all these things sound reasonable FoG and the answer is acceptable. If I remember correctly (I am rusty on these) the reason is that when you switch from 1 to 2 defending armies in an area, you gain the most "benefit" you can gain by adding one defensive unit anywhere. And this is more or less clear by the general principle in the beginning of the game, to locate the area that you are interested in, and in that area place 2 units in every country and then concentrate all the units in one big stack.
However another thing I want to stress, is that we can not treat these numbers commutatively. For instance if we have 4 units and we are about to attack 2 territories which are guarded by 1 and 2 units, and we have a choice in the order in which to attack, then, if we first attack the country which is guarded by 2 units and then the country which is guarded by 1 unit, we as attackers will lose with probability about 47.415 %, while if we perform the attack the other way around (first the country with 1 unit and then the country with 2 units) then the probability of losing such an attack is about 48.892%. This should be easy for you to verify now.
____________
The empty set
|
|
Corribus


Hero of Order
The Abyss Staring Back at You
|
 posted May 14, 2010 08:50 PM
posted May 14, 2010 08:50 PM |
|
|
Q15. 100 Prisoners and Light Bulb.
There are 100 prisoners in solitary cells. There's a central living room with one light bulb; this bulb is initially off. No prisoner can see the light bulb from his or her own cell. Every day, the warden picks a prisoner equally at random, and that prisoner visits the living room. While there, the prisoner can toggle the bulb if he or she wishes. Also, the prisoner has the option of asserting that all 100 prisoners have been to the living room by now. If this assertion is false, all 100 prisoners are shot. However, if it is indeed true, all prisoners are set free and inducted into MENSA, since the world could always use more smart people. Thus, the assertion should only be made if the prisoner is 100% certain of its validity. The prisoners are allowed to get together one night in the courtyard, to discuss a plan, but once visits begin, they may not communicate. What plan should they agree on, so that eventually, someone will make a correct assertion?
Just to make this more interesting for the math whizzes: using your strategy, what is the probability that the prisoners will have been picked within 2 years?
(I'll post a link to a solution some time later.)
|
|
Ecoris

  
    
Promising
Supreme Hero
|
 posted May 15, 2010 12:15 AM
posted May 15, 2010 12:15 AM |
|
Edited by Ecoris at 00:25, 15 May 2010.
|
I've found a strategy that works. It goes like this:
The prisoners are numbered 1,2,...,100. Each prisoner has to keep track of the days and maintain a list of other prisoners they know have been to the living room.
When prisoner number P is picked out on day D he or she has to do as follows:
1) Subtract 100 from D until a number in the range 1,2,...,100 is obtained. Let N denote this number.
2) If the light bulb is on it means that prisoner N-1 has already been to the living room. In that case prisoner P adds N-1 to the list of prisoners he knows have been to the living room.
3) If prisoner P knows that prisoner N has been to the living room he leaves the light on; otherwise he turns it off. (Note that P = N is a likely option).
Eventually some prisoner will know that all prisoners (including himself) have been to the living room. He can then assert that with 100% certainty.
This strategy seems rather slow, but I'm not sure whether it can be done better. They will remain in prison for many many years. Best case scenario is 199 days, e.g.:
1,100,3,100,5,100,...,99,100,any,2,100,4,100,6,100,...,96,100,98,100
A viable alternative would be to compute how many days they have to wait to be at least 99% sure that they have all been to the living room and then simply wait that many days. That should be faster on average. (Of course, they could agree on something else than 99%).
____________
|
|
Corribus


Hero of Order
The Abyss Staring Back at You
|
 posted May 15, 2010 01:10 AM
posted May 15, 2010 01:10 AM |
|
|
I would like to add a clarification.
On a given day, each prisoner knows only whether he has been picked or not. If he hasn't been picked, he has no idea which prisoner has been picked - only that it isn't him. The prisoners cannot communicate in any way after the "game" begins. (By the way, this is more of a logic puzzle than a math puzzle).
For the harder part of the question, I mean something like this:
One of the prisoners, a statistician, suggests that the ideal solution proposed by the other prisoners (i.e., the answer) is too complicated and will take too long. He proposes that after two years, they just declare that everyone has visited the room at least once, and take their chances. What are the odds after two years that they will be released?
It would also be interesting to calculate how long, on average, the "full proof" method would take.
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
friendofgunnar

    
     
Honorable
Legendary Hero
able to speed up time
|
 posted May 15, 2010 09:02 AM
posted May 15, 2010 09:02 AM |
|
|
Each prisoner has a 1 percent chance of being picked each day, which means he has a 99 percent chance of not being picked. So after N number of days the chance of a specific prisoner not being picked is .99 ^ N. So 1 - (.99 ^ N) is the chance of being picked at least once.
1 - .99 ^ N
Now if you had a massive prison complex with 100 different prisons and 100 prisoners in each prison and you identified one random prisoner from each prison to form the 100 then the chance that each of the 100 prisoners had been picked by N days would be (1- .99 ^ N) ^ 100. At 730 days that would be:
0.93693828715108757201755295036561
That doesn't work though if they are in the same prison. If prisoner #1 has been picked at least once it reduces the chances that all the other 99 prisoners have been picked. So the final chance looks like this:
1 * (1- .99 ^ N - 1) * (1- .99 ^ (N-2)) ...((1- .99 ^ N -99)
I'm not sure if there's any way to simplify this series.
BTW The first term in the series is 1 because at least one person has to be picked at least once. You can verify it by looking at the last term. At N = 99 days the last term looks like this:
((1- .99 ^ N -99)
((1- .99 ^ 0)
((1- 1) = 0
which means the entire series equals zero percent chance.
The "logical" solution to the problem is of course a lot easier 
|
|
Ecoris

  
    
Promising
Supreme Hero
|
 posted May 15, 2010 12:40 PM
posted May 15, 2010 12:40 PM |
|
Edited by Ecoris at 12:42, 15 May 2010.
|
Your formula is incorrect, FriendOfGunnar. There is something wrong in your interpretation of conditional probabilities. Just try it with just 3 prisoners and N = 3.
I looked at it like this: Let D denote the day and let X_D denote the number of different prisoners that have been to the living room by day D. We are interested in calculating P(X_D = 100) for all values of D. (P(X_D = 100) is the probability that X_D = 100).
In general, there are two ways that there can have been N different prisoners at the living room by day D:
1) There have been N-1 different prisoners during the first D-1 days and at day D some prisoner is selected for the first time.
OR
2) There have already been N different prisoners during the first D-1 days and at day D some prisoner that has already been to the living room is selected again.
This gives us the following recursive formula:
P(X_D = N) = (100 - (N-1))/100 * P(X_D-1 = N-1) + N/100 * P(X_D-1 = N)
With the initial values
P(X_D = 1) = 0.01^(D-1)
P(X_1 = N) = 0 for N > 1
I generated a large table in excel to compute the values of P(X_D = 100). They are plotted below

Specific values:
P(X_730 = 100) = 0,936796373 (730 days is two years)
P(X_916 = 100) = 0,990002926 (they have to wait 916 days to be 99% sure to be released)
____________
|
|
friendofgunnar

    
     
Honorable
Legendary Hero
able to speed up time
|
 posted May 15, 2010 01:30 PM
posted May 15, 2010 01:30 PM |
|
|
Hmmm, okay
For the other side of the puzzle you can just tell the first prisoner to unscrew the bulb 99/64 full turns (a full turn being 360 degrees). Whenever a prisoner comes to the room for the first time he turns the bulb 1/64 of a full turn. When the last person adds his 1/64 the bulb should come on and the prisoner can inform the jailor that everybody's been to the room. Or you can say that instead of it being turned on it's fully tightened.
|
|
Corribus


Hero of Order
The Abyss Staring Back at You
|
 posted May 15, 2010 04:09 PM
posted May 15, 2010 04:09 PM |
|
|
That's certainly a creative answer, FoG, but how do you expect prisoners with no tools to measure turns with such precision? Not exactly a full-proof strategy. 
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
ihor

 
    
Supreme Hero
Accidental Hero
|
 posted May 15, 2010 04:10 PM
posted May 15, 2010 04:10 PM |
|
|
I believe you guys misunderstood Corribus' task.
Ecoris, you solved the problem like this:
What is the probability, that within D days(730 in particular situation) all of the prisoners will visit living room.
But the task was to find the probability, that within 730 days one of the prisoners will be 100% sure that everybody else have already been in the living room before(everything in the bounds of your strategy).
That is quite different things.
@FoG
It is obvious that, screwing the bulb is illegal. Presence the bulb in the living room gives every prisoner only 1 bit of information: either it is ON, or OFF.
I'll post my strategy:
So in the courtyard prisoners choose one person - lets call him leader. His task will be to count prisoners and finally only leader could say that everybody else have already been there. So strategy:
1)If leader visits living room and bulb is OFF he does nothing.
2)If leader visits living room and bulb is ON, he turns the bulb OFF and increase counter by 1. (Initial value of counter is 1 - means only leader have visited living room).
3)If leader visits living room, bulb is ON and he increases his counter to 100 he says: "Hey guys, everybody of the prisoners was here. You should set us free."
4)If not-leader visits living room first time and bulb is OFF, he turns the bulb ON.
5)If not-leader visits living room, but he have already turned the bulb ON or if the bulb is ON he does nothing.
To help get it what is going on I'll give next example:
Let 1,2,..., 100 - prisoners, 1 - leader. And the random visiting order is 1,2,3,1,2,4,2,1...
1 - leader sees the bulb is OFF(initial value) - does nothing. Counter = 1.
2 - not-leader sees the bulb is OFF and he is first time here, he turns the bulb ON.
3 - bulb is ON - does nothing.
1 - leader sees the bulb is ON - he turns it OFF. Counter = 2.
2 - the bulb is OFF but nr. 2 have already turned it ON once so he does nothing.
4 - turnes ON.
2 - does nothing.
1 - turnes OFF. Counter = 3.
And so on...
For now I have no idea how to calculate the probability mentioned in the second part of task  . But I hope my strategy will help you guys. . But I hope my strategy will help you guys.
|
|
Ecoris

  
    
Promising
Supreme Hero
|
 posted May 15, 2010 05:01 PM
posted May 15, 2010 05:01 PM |
|
|
@ ihor
I provided a strategy yesterday. In the next post Corribus added the question about the statistician which I then answered.
("One of the prisoners, a statistician, suggests that the ideal solution proposed by the other prisoners (i.e., the answer) is too complicated and will take too long. He proposes that after two years, they just declare that everyone has visited the room at least once, and take their chances. What are the odds after two years that they will be released?")
Your strategy is probably faster than mine, ihor. But the only reasonable way to determine the average time to release is through simulations. And I haven't had time to do that yet.
____________
|
|
ihor

 
    
Supreme Hero
Accidental Hero
|
 posted May 15, 2010 06:21 PM
posted May 15, 2010 06:21 PM |
|
|
Yeah, sorry I missed that post  . .
It is correct.
|
|
friendofgunnar

    
     
Honorable
Legendary Hero
able to speed up time
|
 posted May 15, 2010 08:01 PM
posted May 15, 2010 08:01 PM |
|
|
@ Corribus, from the way you phrased your question "While there, the prisoner can toggle the bulb if he or she wishes." I really thought that's the answer you were angling for. 
I was thinking that it's true that 1/64 is impractical but 1/8 isn't. Fooling with the bulb in this way would allow prisoners to pass 8 bits of info (two full revolutions) on to the next person instead of just 1, which could prolly shave centuries off the current schemes.
also, once you introduce practicality into the equasion you start to wonder if 100 random prisoners kept in solitary could stay sane enough to pull the entire thing off anyway. 
|
|
dimis

   
    
Responsible
Supreme Hero
Digitally signed by FoG
|
 posted May 15, 2010 08:37 PM
posted May 15, 2010 08:37 PM |
|
Edited by dimis at 01:42, 16 May 2010.
|
The Coupon Collector Problem
Problem: Given N coupons that are drawn with replacement, each coupon having the same probability of being selected, we want to find out:
(a) When are we expected to draw all coupons.
(b) What is the probability after k trials to miss at least one coupon.
This is a well-known problem, that appears frequently in statistics and in randomized algorithms, so I am not really sure if the guy who proposed the solution is a statistician by default.  Anyway ... Anyway ...
(a) Split the entire period of selecting all N prisoners to N different epochs. Every epoch lasts t_i days, and in that epoch only 1 new prisoner is selected. In other words, t_i is the amount of days to observe a new prisoner once (i-1) have been observed in the past. Then the total number of days T of selecting all N prisoners is the sum of all the t_i's.
However, each of the t_i's comes geometrically distributed since the probability of selecting a new prisoner, once (i-1) have been selected in the past, is
p_i = (N-(i-1)) / N
(Note that in each epoch, it is as if we are tossing a coin with Prob[ Heads ] = p_i and we are interested in the t_i which is the first time Heads will appear.)
So, we have (the first equality by linearity of expectation)
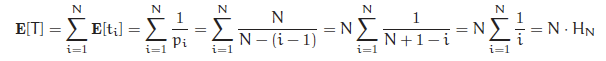
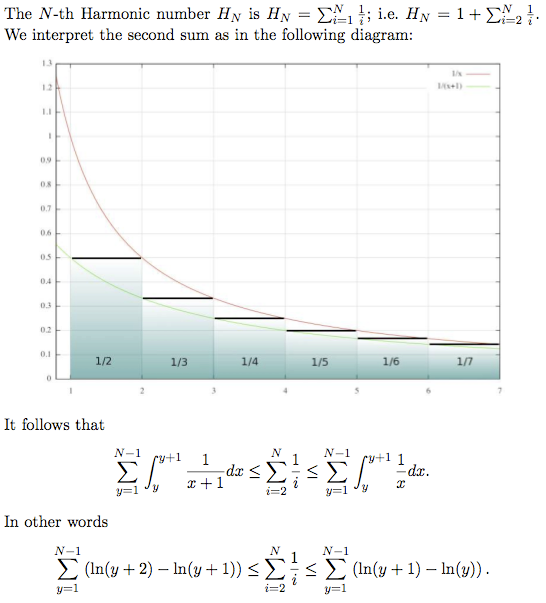
where H_N is the N-th harmonic number.
The N-th harmonic number H_N is usually approximated by the quantity ln(N), since the following inequalities hold
ln(N+1) <= H_N <= 1 + ln(N)
The last inequalities give 4.6151 <= H_N <= 5.6052, or in other words a crude expectation somewhere between 461 days and 561 days. The exact number is computed if we know the exact value for H_N; given that there are 100 guys, this can be done quickly. The right value for H_N is about 5.1874, and hence the expectation is 518-519 days.
(b) We also want to know the probability of missing at least one guy (coupon) after k days (trials).
The first idea is to compute the variance in a manner similar to the one above, and then apply the second moment method (Chebyshev inequality). However, we can do better. (The variance is of order N^2.)
Let A_i be the event that prisoner (coupon) i is not selected within the first k days. This will happen with probability
P_i = (1 - 1/100)^k
Now, the standard "trick" is to use the fact that
1 - x <= e^{-x}
and hence the above probability is bounded from above by
P_i <= e^{-k/100}.
The second step of the standard approach is to make k big enough, so that all the P_i's for the different i's are small, in the sense that the union bound can give good guarantees. In other words
Prob[ T > k ] = Prob[ any event A_i happens ] = Prob[ union of A_i's ].
By the Union Bound, the probability of a union of events is at most the sum of the probabilities of these events, and hence we get
Prob[ T > k ] <= SUM ( P_i ) <= SUM ( e^{-k/100} )
The last sum is 100*e^{-k/100}, so substituting k=730, we get 100*e^{-7.3} which is about 0.0675538 or in other words about 6.76%.
Hmmm.... perhaps the guy who proposed the 2 years time is indeed a statistician. 
I would probably go with a little bit more time.
* 2.5 years => 1.084%
* 3.0 years => 0.176%
* 3.5 years => 0.028%
Another idea above is to set k=c*N*ln(N)=c*100*ln(100) and then 100*e^{-k/100} becomes 100*100^{-c}=100^{-c+1}, and now try to find the appropriate c that makes everyone happy with the end bound on the probability. Then, back substitution on k=c*100*ln(100)=460.517*c, and whatever this gives.
Finally, this problem has a so-called "sharp-threshold" result, in the sense that as n goes to infinity
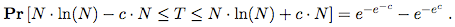
This means that as c increases the probability rapidly approaches 1. In other words, with extremely high probability, the number of trials for collecting all N coupons is very very very close around its expected value. This justifies the name "sharp-threshold", since the result is now almost deterministic although the entire process is randomized.
____________
The empty set
|
|
dimis

   
    
Responsible
Supreme Hero
Digitally signed by FoG
|
 posted May 16, 2010 12:06 AM
posted May 16, 2010 12:06 AM |
|
Edited by dimis at 00:09, 16 May 2010.
|
Approximating Harmonic Numbers
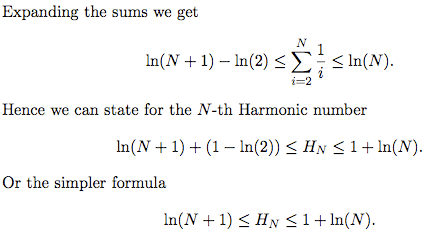
____________
The empty set
|
|
Corribus


Hero of Order
The Abyss Staring Back at You
|
 posted May 16, 2010 12:39 AM
posted May 16, 2010 12:39 AM |
|
Edited by Corribus at 00:40, 16 May 2010.
|
Ihor's answer is the one I was looking for.
By the way, you can read more about the problem here.
And there's a solution to the "harder" part here.
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
dimis

   
    
Responsible
Supreme Hero
Digitally signed by FoG
|
 posted May 16, 2010 12:53 AM
posted May 16, 2010 12:53 AM |
|
Edited by dimis at 01:11, 16 May 2010.
|
I would suggest for the probabilistic proof to go with my proof, since it is easier in the sense that we compute good bounds with a few calculations, while the link requires brute force computation of all the terms in the sum. In the end, if you check my bounds for 2 and 3 years, you can see how close I am without iterating anywhere.
There are two good approximations
* 1-x <= e^{-x}
* H_N about ln(N)
and the basic idea of the union bound.
These are the three things that should remain after the problem.
Btw, we could have used the approximation
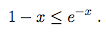
for the birthday problem that FoG solved in the past with an Excel sheet [problem@page 7 and solution@page 8]. I think I didn't mention that in the past. Try it and see what you get!
____________
The empty set
|
| |
|
|





