|
|
Binabik

   
     
Responsible
Legendary Hero
|
 posted February 17, 2010 07:34 AM
posted February 17, 2010 07:34 AM |
|
|
Yes you had the right formulas.
____________
|
|
dimis

   
    
Responsible
Supreme Hero
Digitally signed by FoG
|
 posted February 20, 2010 01:05 AM
posted February 20, 2010 01:05 AM |
|
|
Gender Bias
I don't know where to post it, so I will do it in one of my threads. After all, it shouldn't be *that* off topic.
Gender Bias Bunk, Christina Hoff Sommers, Forbes.
____________
The empty set
|
|
Vlaad

     
     
Admirable
Legendary Hero
ghost of the past
|
 posted February 20, 2010 04:11 AM
posted February 20, 2010 04:11 AM |
|
|
|
An infinite number of mathematicians walk into a bar. The first one orders a beer. The second orders half a beer. The third, a quarter of a beer. The bartender says "You're all crazy", and pours two beers.
|
|
Binabik

   
     
Responsible
Legendary Hero
|
 posted February 20, 2010 05:19 AM
posted February 20, 2010 05:19 AM |
|
|
"You're all crazy"
Do you mean that as "All of you are crazy", or "You are entirely crazy"?
The below space reserved for a more serious off topic discussion about the lack of hot chicks in the sciences.
-------------------------------------------------------
|
|
AlexSpl

   
    
Responsible
Supreme Hero
|
 posted March 03, 2010 12:37 PM
posted March 03, 2010 12:37 PM |
|
|
Is Riemann hypothesis proved? And where can I find updated list of all non-solved mathematical problems?
____________
|
|
Corribus


Hero of Order
The Abyss Staring Back at You
|
 posted March 03, 2010 03:28 PM
posted March 03, 2010 03:28 PM |
|
|
Here is one list.
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
ihor

 
    
Supreme Hero
Accidental Hero
|
 posted March 03, 2010 07:18 PM
posted March 03, 2010 07:18 PM |
|
|
I guess no.
Look at the Millenium Prize Problems, though Poincare Conjencture was proved by Perelman few years ago, don't sure about the others.
|
|
ihor

 
    
Supreme Hero
Accidental Hero
|
 posted March 16, 2010 09:45 PM
posted March 16, 2010 09:45 PM |
|
|
How many different 'words' can you get if you can rearrange letters of word ANTARCTICA?
Every combination of letters is considered as word.
____________
Your advertisement could be
here only for 100$ per day. 
|
|
ohforfsake

  
     
Promising
Legendary Hero
Initiate
|
 posted March 16, 2010 09:55 PM
posted March 16, 2010 09:55 PM |
|
|
Are the A's, T's, etc. different, or can't one differ them? I'd guess they can't be differed, but you wrote each letter, so I got confused. 
____________
Living time backwards
|
|
Corribus


Hero of Order
The Abyss Staring Back at You
|
 posted March 16, 2010 10:18 PM
posted March 16, 2010 10:18 PM |
 bonus applied by Mytical on 19 Apr 2010. bonus applied by Mytical on 19 Apr 2010. |
Edited by Corribus at 22:26, 16 Mar 2010.
|
The original question asked in the VW Probability Thread was a simple one.
If a game has a 25% chance of being "won" and a 75% chance of being "lost", what is the probability of losing the game 10 times in a row?
The probability is calculated as the probability of a single loss raised to the power of number of repititions, or 0.75^10.
A harder variation was: in the same scenario, what is the probability of winning one (and only one) time in those 10 trials?
The probability of X is simply calculated as the total number of ways X can happen, divided by the number of ways ANYTHING can happen. In this case, it was rightly pointed out that there are ten ways to win once.
WLLLLLLLLL, LWLLLLLLLL, LLWLLLLLLL, etc..
Each of these scenarios has the same probability: 0.25*0.75^9. Since there are ten ways it can happen, the total probability of winning once and only once is 10*0.25*0.75^9, or ~19%.
However, the question remains: can we solve the question more generally? What is the most likely number of times you will win when playing this game 10 times. A quick answer that should make sense is: if the probability of winning the game is 25%, then you should win 25% of the time. Out of ten games, your most likely expected result is therefore 2.5 times.
Does this bear out?
First, we need a more general formula for our probability. So let's take the more challenging case of exactly TWO wins. What are the ways this can happen? We could win the first and second games, and lose all the rest. We could win the First and third games, and lose #2 and #4-10, etc.
I.e. for wins, we could have 1,2; 1,3; 1,4; 1,5; 1,6; 1,7; 1,8; 1,9; 1,10; Also possible is 2,3; 2,4; 2,5; etc. Notice that we don't repeat 2,1, because that's the same as 1,2.
Anyway, if you add all of them up, you will find we have 45 possible ways we could win two games. So the probability of winning two games is: 45*0.25^2*0.75*8, or ~28%.
Well, this would get tedious trying to do 3 wins, so there's actually an easy formula.
If we call the probability of a win pw (0.25) and the probability of a loss pl (0.75), and the number of wins and losses nw and nl, respectively (where nw + nl = N, the total number of games), then the probability of winning w times (Pw) is:

The second equation is just a handy check. That is, if we add up the probability of winning once, plus the probability of winning twice, etc. through all the possibilities, we should get unity.
The factorials result from what is known as a combination without repetition. You can read more about them here. In "game math", we often refer to those combinations as "X choose Y". In the case of N = 10 (our original problem), the probability of winning twice would be 0.25^2*0.75^8 * "10 choose 2", or 10!/(2!8!), or 45.
Anyway, I plotted out the Pw values (in percent) as a function of nw:
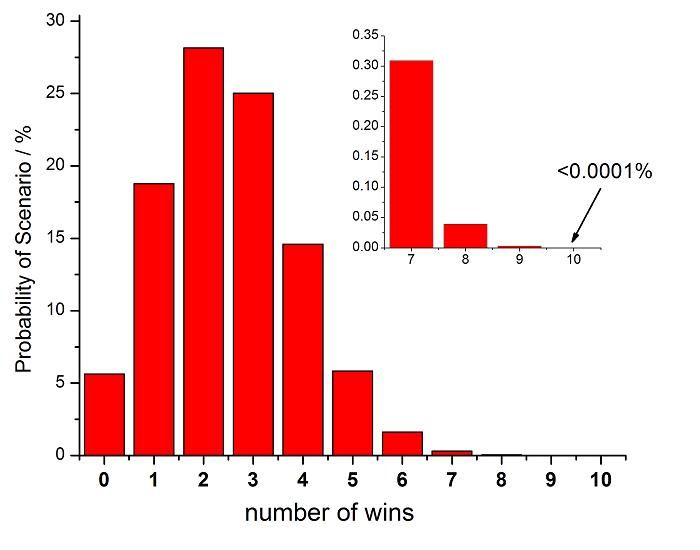
As you can see, the most likely value falls somewhere between 2 and 3.
Note that this equation is easily modified for other games. For instance, if we chance the number of repetitions to 100 and change the probability of winning to 1/2 (say, a coin flip) or 1/6 (say, a die roll), you can see how the result changes:
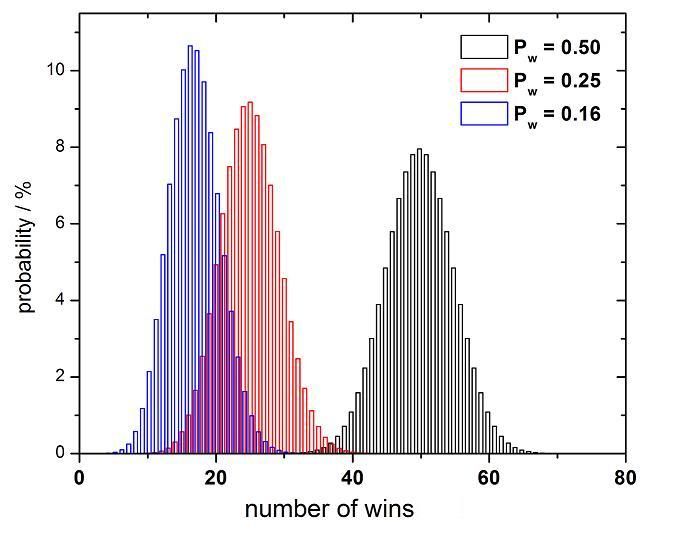
Not surprisingly, the results are gaussian, or a normal statistical distribution. Also you can see that the gaussian function peaks at whatever the probability of winning is. For example, the most likely result of 100 coin flips is 50 "wins" (heads, say). Also, if you have to roll a 6 on a 6-sided die to win, you can see that this happens approximately 16 times in a hundred rolls.
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
ihor

 
    
Supreme Hero
Accidental Hero
|
 posted March 16, 2010 10:49 PM
posted March 16, 2010 10:49 PM |
|
|
@Ohforf
Of course if exchange two A's the word will remain the same.
Example: the same problem for word ABA
1)ABA
2)AAB
3)BAA
Answer: 3.
BTW I don't know the answer for ANTARCTICA, I just know the method. I choosed random long word with multiple letters.
@Corribus
I don't understand what was the purpose to make such a research. 
|
|
Corribus


Hero of Order
The Abyss Staring Back at You
|
 posted March 16, 2010 10:51 PM
posted March 16, 2010 10:51 PM |
|
|
Recently bought a new version of Origin. Trying to learn how to use it. This seemed like a nice test case. You should have seen all the figures I did NOT post. 
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
ihor

 
    
Supreme Hero
Accidental Hero
|
 posted March 17, 2010 08:04 AM
posted March 17, 2010 08:04 AM |
|
|
At the university where I'm studying two math programs installed:
Maple and Mathematica.
I can handle only with Maple, but this is indeed useful, multifunctional utility. Sometimes it helps a lot  . .
|
|
AlexSpl

   
    
Responsible
Supreme Hero
|
 posted March 17, 2010 08:32 AM
posted March 17, 2010 08:32 AM |
|
|
Quote:
Recently bought a new version of Origin
Try also Wolfram Mathematica 
____________
|
|
Corribus


Hero of Order
The Abyss Staring Back at You
|
 posted March 17, 2010 02:32 PM
posted March 17, 2010 02:32 PM |
|
|
I have Maple (at home) and Mathematica (at work). Origin is a completely different program - more for data analysis, statistics and plotting. Unfortunately, they have a tendency to completely change everything with each new edition, so there's a steep learning curve every time I get a new version.
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
ohforfsake

  
     
Promising
Legendary Hero
Initiate
|
 posted March 24, 2010 03:37 PM
posted March 24, 2010 03:37 PM |
|
|
Set theory; Russels Paradox, I don't see the paradox
Okay, so according to wikipedia, Russels Paradox goes like this:
Define sets which are contained in themselves, as 'abnormal' and sets that aren't contained in themselves as 'normal'.
Assume you want to collect all 'normal' sets in one set, and only 'normal' sets.
Doing this, you get the problem of what type of set, is the set of all 'normal' sets. If the set is 'normal' it doesn't contain itself, and thereby don't contain all 'normal' sets. If the set is 'abnormal', it does contain itself, but doesn't only contain 'normal' sets then.
The same type of problem does one meet in the case of the barbar who shaves all in town that doesn't shave themselves.
Because who shaves the barber then? If the barbar shaves himself, then he shaves someone that does shave himself, and if the barber doesn't shave himself, then there are one the barbar doesn't shave, who doesn't shave oneself.
I however don't understand why this is a paradox? To me it sounds more like an impossibility.
Let me try to explain, first with the 'normal' / 'abnormal' sets then with the barber example.
If one tries to construct the set of all 'normal' set, one could first take all 'normal' sets in the world, except one, the set of all 'normal' set, and collect them in one set.
Now there's no doubt that we've collected all 'normal' sets there exist, except for the set of all 'normal' set.
We however want all 'normal' sets, so we let the set of 'normal' sets (the set we've already created) be included in this set.
This however makes the set 'abnormal', so we've now all 'normal' sets in one 'abnormal' set.
All there's to this, in my opinion, is that it's impossible to create a set of all 'normal' sets, which is clear when trying to construct such, you can either have all, except one, 'normal' set in your set, or you can have all 'normal' sets and at least one 'abnormal' set.
The same goes with the barbar, the barber goes start by collected all who doesn't shave themselves, except the barbar self. Now it is clear, that either the barbar can shave all who doesn't shave themselves, except the barbar self, or can shave all who doesn't shave themselves and the barbar self included.
I don't understand why it is a paradox, when defining an entity that changes properties upon construction and then try to construct it in a way that goes against the definition, making it impossible.
It is like the statement, I lie, telling the truth, and one would not be lying, lying and one would be telling the truth, thereby not be lying, it is thereby impossible to do, but I don't see why it is a paradox.
____________
Living time backwards
|
|
ihor

 
    
Supreme Hero
Accidental Hero
|
 posted March 24, 2010 05:05 PM
posted March 24, 2010 05:05 PM |
|
|
This is not impossibility. Theorerically you can build a set, that consists of all sets that doesn't include themselves. Can't you? Theoretically you can do almost everything 
The paradox is this set can't include itself while it also must include itself.
I don't remember all the details around this paradox, but as I remember it started boom in mathematical circles around definitions of set, so there will not arise any paradoxes, which leaded to assuming a set as prime non-definable object.
|
|
ohforfsake

  
     
Promising
Legendary Hero
Initiate
|
 posted March 24, 2010 05:15 PM
posted March 24, 2010 05:15 PM |
|
|
Quote:
Theorerically you can build a set, that consists of all sets that doesn't include themselves. Can't you?
I don't think you can, try to build it.
The way I'd build such a set, is first to take all 'normal' sets and place them together, except the set of all 'normal' sets (the set we just constructed).
Now we can either choose to:
1) Add the set to itself, creating a set of all 'normal' sets and one 'abnormal' set, making the set 'abnormal'.
2) Not add the set to itself, thereby having created the set of all 'normal' set, except the set itself.
Quote:
The paradox is this set can't include itself while it also must include itself.
Which I only thinks arises when realising such a set is impossible to build upon the definitions it is made. It is defined in such a way, that when adding it to itself, you'll not get the set of all and only 'normal' sets, and when not, you'll also not get the set of all and only 'normal' sets, because the action of adding the set to itself changes its properties according to the definition we're applying.
Quote:
but as I remember it started boom in mathematical circles around definitions of set, so there will not arise any paradoxes, which leaded to assuming a set as prime non-definable object.
All I remember about the history behind the problem, is that it lead to suggestions for other set theories at which such paradoxes were avoided (which I'd still call impossibilities and not paradoxes.  ). ).
____________
Living time backwards
|
|
ihor

 
    
Supreme Hero
Accidental Hero
|
 posted March 25, 2010 07:42 AM
posted March 25, 2010 07:42 AM |
|
|
Quote:
I don't think you can, try to build it.
There is one controversial axiom - axiom of choice(AC), which generally says that given any collection of bins, each containing at least one object, it is possible to make a selection of exactly one object from each bin. It means that if you include this axiom you can build a set A in following way: you can examine every single set X and if X include X then add X to A.
Build set A would be paradoxal in the meaning of said before.
But you can do it only if AC is included.
|
|
Ecoris

  
    
Promising
Supreme Hero
|
 posted March 25, 2010 06:35 PM
posted March 25, 2010 06:35 PM |
|
|
Quote:
This is not impossibility. Theorerically you can build a set, that consists of all sets that doesn't include themselves. Can't you?
No. You can't. The axioms of set theory do not allow a set to be a member of itself.
Quote:
There is one controversial axiom - axiom of choice(AC), which generally says that given any collection of bins, each containing at least one object, it is possible to make a selection of exactly one object from each bin. It means that if you include this axiom you can build a set A in following way: you can examine every single set X and if X include X then add X to A.
Build set A would be paradoxal in the meaning of said before.
But you can do it only if AC is included.
This makes no sense. The axiom of choice has nothing to do with Russell's Paradox.
____________
|
| |
|
|





