|
| Thread: The Science of Small |  This thread is pages long: 1 2 3 4 · «PREV / NEXT» |
|
titaniumalloy
Honorable
Legendary Hero
Professional
|
posted October 28, 2009 06:56 AM |
|
|
Corribus, out of curiousity, what did you study at University? I think you mentioned it before but I forgot where.
____________
John says to live above hell.
|
|
Geny
Responsible
Undefeatable Hero
What if Elvin was female?
|
|
posted October 28, 2009 10:10 AM |
|
|
The last part was most interesting. Waiting for more. 
____________
DON'T BE A NOOB, JOIN A.D.V.E.N.T.U.R.E.
|
|
TheDeath
Responsible
Undefeatable Hero
with serious business
|
|
posted October 28, 2009 03:58 PM |
|
|
I have a hard time grasping the fact that both powders & hard materials are made from particles -- it's not like the hard material is a bigger particle really, it's also made from smaller ones... so "cutting it into pieces" isn't a correct way to understand this since you actually only separate some connections (right???), it's confusing to imagine.
I mean, intuitively of course, cause I know how it is "in reality", but can't quite "get it". 
____________
The above post is subject to SIRIOUSness.
No jokes were harmed during the making of this signature.
|
|
Corribus
Hero of Order
The Abyss Staring Back at You
|
|
posted October 28, 2009 11:41 PM |
|
|
@TA
Quote:
Corribus, out of curiousity, what did you study at University? I think you mentioned it before but I forgot where.
My degree is officially in chemistry but molecular physics would probably be a better description of my expertise.
@Death
I'm having a hard time understanding what you're asking. I sort of get it, but I'd like you to clarify your question before I try to answer it. Perhaps an example would help.
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
TheDeath
Responsible
Undefeatable Hero
with serious business
|
|
posted October 28, 2009 11:45 PM |
|
|
"Intuitively", most of the 'size' of the atom is empty space. And everything is obviously made up of molecules, so the 'surface' area is more like a collective of particles. The thing is that there are no "bigger objects" with this imagination, since they are made up of particles just like the smaller objects, with most of it being empty space (obviously, I know there are connections, but I'm saying intuitively only it's hard to grasp , not that I don't get it).
____________
The above post is subject to SIRIOUSness.
No jokes were harmed during the making of this signature.
|
|
winterfate
Supreme Hero
Water-marked Champion!
|
|
posted October 29, 2009 12:10 AM |
|
|
@Corribus: Awesome read! 
Interesting you should mention the anti-cancer nanites, considering I'm taking Immunology this semester.
I got an 89% on the first test. So close yet so far to the A. 
____________
If you supposedly care about someone, then don't push them out of your life. Acting like you're not doing it doesn't exempt you from what I just said. - Winterfate
|
|
Kareeah_Indaga
Responsible
Undefeatable Hero
|
|
posted October 29, 2009 01:37 AM |
|
|
Quote:
The first thing you’ll notice from the figure is that the data is not randomly scattered around the plot: there’s a clear inverse correlation between peoples’ perceptions of the risks of technologies and their potential benefits. With the exception of firefighting (FF) and police work (PW), technologies tend to either be high risk, low benefit or low risk, high benefit. For some technologies, such as solar power, this is sensible. Obvious benefits there, especially with all the global warming and “fossil fuels = bad” press that’s around right now. On the other hand, the rankings of some technologies don’t really make sense. Asbestos, for instance. Certainly, the health concerns of asbestos are serious (though, to be fair, a bit overstated), but on the other hand, asbestos does have a lot of benefits. Its fireproofing capacity (especially versus cost) is quite useful. So why do people perceive the benefit of asbestos is low? My guess is that there’s an evolutionary answer buried in there somewhere, but nevertheless, the data clearly show that when people get it into their heads that something is potentially harmful, they also tend to perceive that it is (proportionately) less useful. In other words, there’s a psychological tendency to undervalue the potential benefits of risky behaviors – and, vice-versa, for to undervalue the risks of clearly beneficial behaviors.
*cough*halo effect*cough*reverse halo effect*cough*
____________
Adventures in Helnith has moved!
|
|
Corribus
Hero of Order
The Abyss Staring Back at You
|
|
posted October 29, 2009 02:20 AM |
|
|
@Death
Well everything is particles made of particles made of particles. Chemical reactions are little more than the changing of the position of electrons from one place to another. Those motions are determined by electrostatic forces, forces which are highly dependent on distance and the interaction with other nearby charges. It can therefore hardly be expected that electrons located in the center of a lump of iron would be transferred, say, to a nearby oxygen molecule, than would be electrons at the surface of a lump of iron. An it's pretty clear that as the size of the lump of iron gets smaller, there is a larger ratio of surface-area to volume, meaning there are more electrons available for transfer to nearby reactants.
And also, when we say "nanoparticle" or "particle size" when referring to little bits of matter, we are not talking about the physical definition of particles (say, electrons or protons). By particle in the chemical sense I am referring to "a hunk of atoms bound together by electrostatic interactions" - a chunk of stuff, if you will. In that sense, a lump of coal is a particle, and so is a bucky ball, which is a nanosized lump of carbon. The lump of coal is a larger particle than a bucky ball.
Other than that, I'm still not really sure what your point is.
@Fate
Quote:
I got an 89% on the first test. So close yet so far to the A.
Next time study harder.
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
TheDeath
Responsible
Undefeatable Hero
with serious business
|
|
posted October 29, 2009 02:36 AM |
|
|
For example, a powder (of the same substance) will have less volume for a given "space" than a solid form. It will need more space since it's more "expanded" (otherwise it would have connections between the 'particles' (note: chunks), so it would become a solid), therefore that means less volume per space occupied (or same volume, but more space needed).
Given that it needs a lot of space compared to the solid, the surface-to-volume ratio will be higher than for a solid form, but the surface-to-space ratio will probably not (although of course this is just an example where powder takes up waaaay more space!).
Ok I'm just rambling it's just a bit confusing/counter-intuitive to imagine it, that's all.
(what I'm talking about is the "surface=/=continuous thing" that is hard to get here, and that a 'solid' is actually made of connected molecules & forces, not of 'continuous stuff')
____________
The above post is subject to SIRIOUSness.
No jokes were harmed during the making of this signature.
|
|
Corribus
Hero of Order
The Abyss Staring Back at You
|
|
posted October 29, 2009 04:15 AM |
|
|
Quote:
For example, a powder (of the same substance) will have less volume for a given "space" than a solid form. It will need more space since it's more "expanded" (otherwise it would have connections between the 'particles' (note: chunks), so it would become a solid), therefore that means less volume per space occupied (or same volume, but more space needed).
I see what you're saying, but, well, that difference is fairly negligable until you get to particles with really small size (i.e., to particles that are almost single atoms). Furthermore that space is dead space when it comes to chemical reactions as well, so you can still count it as part of the volume of the solid.
In any case, we're talking qualitatively so even if that was an effect to be concerned with, it wouldn't change the fact that a larger number of smaller particles have more exposed atoms/ions than a smaller number of larger particles with the same overall mass.
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
ohforfsake
Promising
Legendary Hero
Initiate
|
|
posted October 29, 2009 09:35 AM |
|
|
Quote:
Just drop a note saying you read it, though, so I know I'm not just typing all that for myself.
Understood , I'll probably be off for longer periods of time (where I won't be able to post), but when I drop by and reads this thread, I'll make my presence known.
I really appreciate that you give us the opportunity to get a much better perspective than what you'll recieve when reading the common press. I believe you aren't biased towards making a profit somehow via this thread, which the press sadly is, and seem to neglect the purpose of making informations available in turns for higher profit.
|
|
TheDeath
Responsible
Undefeatable Hero
with serious business
|
|
posted October 29, 2009 05:34 PM |
|
|
@Corribus: I know I "get it" that way, but I was talking it's not intuitive to imagine empty space being "a barrier" (for chemical reactions) as well, because a surface being 'continuous' is the intuitive approach. Anyway now thanks for making it a bit more "clear"
____________
The above post is subject to SIRIOUSness.
No jokes were harmed during the making of this signature.
|
|
Corribus
Hero of Order
The Abyss Staring Back at You
|
|
posted November 04, 2009 11:04 PM |
|
Edited by Corribus at 23:13, 04 Nov 2009.
|
Quantum Dots. Part 1
In the previous article, I tried to provide a basic description of why nanoscale materials have unique properties compared to macroscale (“bulk”) analogs composed of the same “stuff”. I boiled down the explanation into two primary reasons: changes in chemistry and changes in physics. The changes in chemistry that occur are fairly easily understood (unless you’re TheDeath ), but when it came to changes in physics, I just sort of waved my hand and said that it’s because of quantum mechanics. And then I moved on.
Well, no longer!
Some of the most important classes of nanomaterials depend upon these changes in physics for their function, and if you want to understand nanotechnology, it’s important to have a better understanding of what is going on in quantum physics, and why those effects become much more important when you get into the nanometer length domain. To that end, this article will discuss quantum dots (QDs), one of the most popular types of nanomaterials that are out there. If you look at any issue of any major publication in just about any subdiscipline of chemistry, you’ll likely find oodles of articles related to quantum dots, either discussing their applications or their fundamental physics.
Semiconductor nanocrystals (quantum dots).
This article will necessarily be heavy on physics, but I will try to present it in a straightforward, nonmathematical way that will hopefully be interesting and informative. I will have to start with the properties of some bulk materials first before moving into the nanoworld. At the end, I’ll briefly present a few of the most promising applications for these materials. This article will be in two parts – the first laying some groundwork in quantum mechanics and semiconductors, and the second using those principles to describe the size-dependent fluorescent properties of QDs and their applications.
Note: I promised this article to Winterfate years ago and I always felt bad about not following through. So, here you go, ‘Fate: my conscience is now clear.
Orbitals, States, and Fluorescence
One of the peculiarities of quantum mechanics is that electrons (well, all particles) cannot have any random velocity, energy or position; the observable properties of quantum particles may only take up certain discrete “quantized” values. Here is an easy way to see why this occurs. Bits of matter – even large ones – in motion have wavelike properties, and the degree of “waveness” becomes greater as the mass decreases. Allowed states of motion are those in which the particle-wave doesn’t cause itself to vanish through destructive interference. In a classical hydrogen atom, a classical electron orbiting a classical proton can have basically any orbit you can imagine because trajectories are essentially Newtonian: the electron has a well-defined position and velocity in time and can circle around the proton at any distance. Not so with a (real) quantum system. Only orbits of certain distances away from the nucleus are permitted because in those which are not permitted, the wave describing the electron interferes with itself. For a quantum state of an electron to be allowed, the electron’s wave has to be a continuous standing wave around the nucleus. For example:
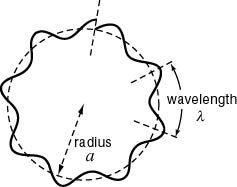
This is a diagram illustrating a “forbidden” quantum state. Note that the wave does not “match up” with itself. An electron in this orbit would essentially destroy itself. Only states in which the wave matches up with itself (a standing wave) are allowed in the quantum system.
It certainly gets more complicated than that, but the important point for the purposes of the following discussion is that electrons are only allowed to occupy certain quantum states which are known in the chemistry world as orbitals. It’s important to understand that these orbitals don’t represent where an electron is or how it moves, but rather represent where it is possible to find the electron if you were to make a measurement at a certain instant in time. Remember: in the quantum world, events are not deterministic. In the classical world, if you know the position of something and its current velocity (and all the forces involved), you can easily determine where the particle will be a certain amount of time later. In the quantum world, physics doesn’t work like this. You can only predict where the particle will be. Reality in the quantum world is probabilistic, not deterministic. Now, wrap your head around that!
Anyway, in a hydrogen atom, as I’ve said, you have a single electron “orbiting” a single proton, sort of like this:
Note that “orbiting” here has a very different meaning from, say, the moon orbiting the Earth. Each orbital, for reasons which are unimportant, can accommodate exactly two electrons. So, in the helium atom, there would be an additional electron in the empty “space” shown in the diagram above. Additional electrons in heavier elements would be filled into other orbitals which usually have more peculiar shapes and longer distances from the nucleus. That’s not really important, but you should know that you can cause electrons to move from a low energy orbital like the one shown here into higher energy orbitals if you supply exactly the right amount of energy – an amount of energy equal to the difference in energy between the two orbitals. In addition, when you excite these electrons into higher orbitals, they will eventually fall back down to their resting positions, and in the process emit photons of (in atoms, anyway) the same color. In a star, such as the sun, hydrogen atoms are heated up to incredibly high temperatures, which results in electrons being excited to all kinds of allowed higher energy states. These excited electrons invariably relax back down, emitting photons of all different colors. Thus, what you can measure if you have the appropriate equipment is an atomic spectrum, such as
The measured spectral lines correspond to transitions between the allowed quantum states in the hydrogen atom. Note that the spectral lines for each element are different, because the allowed states in each element are different. Using this spectral information, astronomers can determine the elemental makeup, age, etc., of stars which are very far away. It is noteworthy that the discrete spectral lines (and their patterns) observed in stellar spectra a significant challenge to Newtonian physics in the late 1800s, and quantum theory arose in part as a way to explain what astronomers were observing with their new telescopes. The eventual success in explaining the complicated patterns of spectral lines was a major early victory for quantum mechanics.
Alright, moving on. If you take two hydrogen atoms and bring them close to each other, you form a hydrogen molecule. There’s a whole branch of theoretical chemistry devoted to understanding what happens to electrons/orbitals when two atoms are brought together, and the most successful theory by far is molecular orbital theory (MOT). What it basically boils down to is that when a molecule is formed from, say, two atoms, the electrons are constricted to molecular orbitals which are formed by combining the atomic orbitals of the constituent atoms, as shown below for the simple hydrogen (H2) molecule:
On the right and left you see the lowest-energy hydrogen atomic orbitals, which are called 1s orbitals. When you bring these together, you form two molecular orbitals. One of these, called the bonging molecular orbital (1sigma) is lower in energy (more stable) than the two isolated hydrogen atomic orbitals; the other orbital, called the anti-bonding molecular orbital (1sigma-star) is higher in energy (less stable) than the two isolated hydrogen atomic orbitals. You have two electrons, and these are both put into the lower energy (bonding) orbital; the result is a net stabilization of the system, which is why a strong chemical bond is formed between two hydrogen atoms to form a molecule. Empty orbitals mix as well, so there are plenty more molecular orbitals for hydrogen than just the two shown in the figure. I don’t want to get too much more into it, so let’s look at the important points and move on:
1) As in atoms, electrons can move between molecular orbitals if the right amount of energy is supplied. The yellow arrow indicates the amount of energy required to promote an electron from the ground (lowest energy) state into the antibonding orbital, which is the H2 molecular orbital with the next-lowest energy. We call this energy the “energy gap”. Note that an electron in the antibonding orbital will relax back down to the bonding orbital (provided there is room for it), emitting a photon of that energy/color in the process. We call this process fluorescence. That is, an excited molecule will fluoresce a color which is related to the energy gap.
2) The energy gap is dependent on a lot of factors, most of which are related to the exact nature of the atomic orbitals, how many electrons they have, and, additionally, the separation between the atoms in the molecule. The little figure at the bottom left hand part of the figure plots the energies of the bonding and antibonding orbitals of H2 as a function of the bond length. The energy gap is the distance between the two red lines. I don’t think I need to say much more about that as it is pretty obvious that the energy gap changes as the atoms move closer together and further apart – and it shouldn’t be a surprise that the interatomic spacing varies from molecule to molecule. Thus, different molecules, like different atoms, would be expected to have different fluorescence colors.
Metals, Insulators and Semiconductors
So now you know what happens to orbitals in molecules. Basically, they are just mathematical combinations of the atomic orbitals surrounding each individual atom in the molecule. The number of molecular orbitals formed is always equal to the number of atomic orbitals that go into the combination. While heavy elements like carbon have oodles of occupied atomic orbitals, and thus large networks of carbon atoms, such as would be found in most organic molecules, would be expected to have dozens, if not hundreds or thousands of occupied molecular orbitals, typically we can get away with only considering a small subset of them – those formed by the highest energy occupied atomic orbitals (which we often call the valence orbitals), because these are the only ones that are likely to have any non-negligible degree of interaction with each other. With that in mind, let’s look at what happens as the number of atoms approaches infinity, as would happen in a bulk material like a polymer or hunk of metal.
Below is an orbital diagram of the organic semiconductor polyacetylene. Here we consider interaction of certain p-orbitals on each carbon. Don’t worry about that detail; for our purposes they can be treated identically as the s-orbitals in hydrogen.
The axis along the bottom is number of carbons. The n = 1 and n = 2 orbital diagram should look pretty familiar now; FYI, the little up and down arrows represent electrons with opposing spins. But look at what happens as the number of carbons gets large. First, you see that the energy gap gets smaller – or, that the fluorescence color would shift to the red. More importantly, you see that all the orbitals get closer and closer together in energy. In the case of an infinite number of atoms, there are an infinite number of orbitals which are (obviously) infinitely close together. It can be seen that half of the orbitals are filled with electrons (red) and half empty (blue). Because at this point it’s hard to think of discrete orbitals – because the orbitals are so close together in energy – we rather refer to “blocks” of orbitals called bands. The filled band is known as the valence band and the empty band is known as the conducting band. Even in the infinite limit, in the case of polyacetylene, there is a space between the bands that has no orbitals. The gap between the bands is known as the “band gap”, and this determines just about every electronic property of a solid material that you can think of.
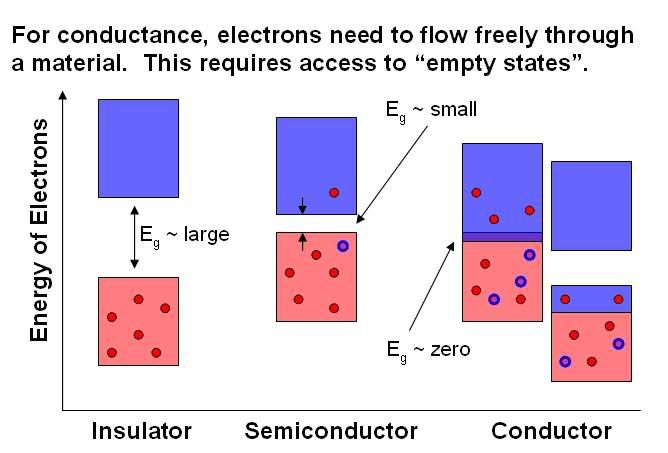
The thing to understand here is that the move around freely, and the ability of electrons to move around is determined by the number of available empty orbitals/states so that they can hop along wherever they want. And guess where the empty orbitals/states are in a material: in the conducting band! So, if electrons can conveniently access the conducting band, you have a conductor; if they can’t, you’ve got an insulator. In a material where the band-gap is very large, there’s not enough latent energy around, even at high temperatures, to promote electrons up into the conducting band, which means that electrons cannot move efficiently and thus means the material is an insulator. In a metal, on the other hand, the two bands often overlap, or are half-filled, which means that there is no band-gap at all. Electrons can flow freely at any temperature, which is why metals conduct electricity very well. The intermediate case is a semiconductor. This is a material with a moderate band-gap – at low temperatures, the material is an insulator, but as the temperature is raised, enough electrons can be promoted by the latent energy into the conducting bands to make the material conducting. Note that insulating materials can be made into semiconductors by doping – that is, replacing some of the atoms in the material with other elements, which has the effect of putting some intermediate states in the band-gap region. Shirokawa, McDiarmid and Heeger won the 2000 Nobel Prize in Chemistry for figuring out how to turn plastics (normally insulating polymers) into semiconducting materials by doing this. The ability to manipulate the conductance properties of semiconductors by temperature, doping, or other methods has made them important components of transistors – giving them paramount importance to the computer industry. And as it so happens, quantum dots are made of semiconducting materials.
Just to drive this point home, here is one more figure on semiconductors which may be useful:
It just shows that as you go down the periodic table from carbon to silicon to germanium, bulk materials composed of these elements become increasingly more conductive because of the shrinking band-gap.
Conclusion
That concludes the “groundwork” phase of this article. Now you are completely equipped to understand quantum dots and why they are useful in a variety of technological applications. I’ll get to that in part 2 of this article.
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
winterfate
Supreme Hero
Water-marked Champion!
|
|
posted November 05, 2009 12:10 AM |
|
|
*is violently reminded of Organic Chemistry and Physics*
But, as long as it helps me understand the next part, it's all good.
Quote:
Note: I promised this article to Winterfate years ago and I always felt bad about not following through. So, here you go, ‘Fate: my conscience is now clear.
I'm just glad you decided to still do the article after so much time.
For that I thank you.
____________
If you supposedly care about someone, then don't push them out of your life. Acting like you're not doing it doesn't exempt you from what I just said. - Winterfate
|
|
TheDeath
Responsible
Undefeatable Hero
with serious business
|
|
posted November 05, 2009 12:40 AM |
|
|
I have to admit the part about infinite atoms is a bit confusing: I didn't know a larger hunk changes the orbits or adds more orbits? Or is it only because I confuse orbitals with something to do with orbits?
BTW where do you get all these pics from, or do you make them yourself? 
____________
The above post is subject to SIRIOUSness.
No jokes were harmed during the making of this signature.
|
|
Corribus
Hero of Order
The Abyss Staring Back at You
|
|
posted November 05, 2009 04:18 AM |
|
Edited by Corribus at 04:20, 05 Nov 2009.
|
@Death
Quote:
I have to admit the part about infinite atoms is a bit confusing: I didn't know a larger hunk changes the orbits or adds more orbits? Or is it only because I confuse orbitals with something to do with orbits?
That's not a terribly easy question to answer, and to do it justice I'd really have to break out some matrix algebra. Which I'm sure nobody wants. I'm sure of the best way to answer the question, so I'm just going to start rambling and see if I hit on anything.
Orbitals (wavefunctions) are graphical representations of where an electron is likely to be found at a given time. They are related to probability distributions, and two-dimensional drawings of them don't really do an adequate job of depicting what they mean. For example, the 1s orbital is often depicted as a circle. Obviously, a better way to depict it would be a spherical shell around the nucleus, but even that is inadequate. The shell only represents the most likely radial position of the electron; in fact the electron has a nonzero probability of being located just about anywhere except at certain locations where the wavefunction is explicitly equal to zero (nodes). For example, it is possible, though unlikely, for an electron to be found three miles from the nucleus to which it is bound. How do you depict that graphically?
But more related to your question: adding more nuclei onto the system both changes the molecular orbitals that already describe the smaller system, and increases the number. Because of the way the math works, the number of molecular orbitals must equal the number of input atomic orbitals (because the molecular orbitals are essentially just linear combinations of the atomic orbitals). An orbital formed by combining 20 orbitals on connected carbon atoms will spatially span all 20 atoms, and an electron contained in such an orbital is “spread” over all 20 atoms. In organic chemistry parlance, we call the electron “delocalized”. Adding additional atoms (hunks) further delocalizes the electron. Of course, when I speak of an “infinite limit”, I do so in a mathematical sense only – often we extrapolate mathematical equations to infinity to see what the limits are for “very large molecules”. There are no molecules with an infinite number of atoms.
In addition, there are practical limits to the distances over which single electrons (orbitals) can be delocalized. These limits come out of the mathematical equations, which are much more complex than the simplistic picture I’ve painted here, as well as the imperfect nature of real materials. Also, things like defects in a perfect crystal lattice, variations in bond lengths, polymer branching, atomic substitutions, etc., all play a role in determining the properties of real systems, which can be often different than idealized systems we use for models. The goal is of course to develop more sophisticated models which can account for these contingencies.
Well, I don’t know if that answered your question or not. In bulk materials, and especially conductors, the orbital concept loses a lot of its rigorous meaning and usefulness because the allowed energy states become almost continuous, all the states are interacting with each other, electrons are easily jumping from state to state, etc. Things are basically so much more complex that it’s hard to model the material properties as being related to a simple combination of atomic orbitals. So, what’s more important than where electrons are is where they aren’t – the band gap, which is determined by an infinite limit extrapolation, and yes, some “basic” quantum chemical models can predict these gaps quite well, even if the specific nature of any individual orbital is impossible to describe.
Quote:
BTW where do you get all these pics from, or do you make them yourself?
Most of them I’ve made myself, although lest you think I have nothing better to do with my time than make a lot of figures for you people, most of them I made in the past for various lectures or talks I’ve had to give.
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
TheDeath
Responsible
Undefeatable Hero
with serious business
|
|
posted November 05, 2009 06:58 PM |
|
Edited by TheDeath at 18:59, 05 Nov 2009.
|
I see, that makes much more sense to me than you might think. The problem is I pictured them as being orbits (not necessarily elliptic mind you), which are 2D or on a single plane, but I had no idea that the "randomness" or "uncertainty" in quantum mechanics of the position of an electron can be that large (like finding one a mile distance, even though extremely extremely unlikely).
So "combining" atoms to form molecules changes the probability distribution of the orbitals (and adds more "valid" orbitals, since it's only quantized states).
____________
The above post is subject to SIRIOUSness.
No jokes were harmed during the making of this signature.
|
|
Corribus
Hero of Order
The Abyss Staring Back at You
|
|
posted November 05, 2009 07:50 PM |
|
Edited by Corribus at 01:02, 06 Nov 2009.
|
@Death
Quote:
I see, that makes much more sense to me than you might think. The problem is I pictured them as being orbits (not necessarily elliptic mind you), which are 2D or on a single plane, but I had no idea that the "randomness" or "uncertainty" in quantum mechanics of the position of an electron can be that large (like finding one a mile distance, even though extremely extremely unlikely).
Well, of course the probability would be so low as to be essentially zero, but the point is that it is not mathemetically equal to zero. There are few places that a particle absolutely cannot be in a real system, and so we usually speak of where an electron is most likely to be rather than where it is allowed to be. An orbital is a probability function that explains, mathematically, where the particle is likely to be found, a time-average if you will. An electron in a certain orbital spends its time at positions specified by the orbital and has associated energy/momentum/etc values determined by the orbital. If you integrate the probability function over all spatial dimensions you get a value of 1. You should also realize that, aside from the orbitals of the hydrogen atom (and other one-electron atoms), all orbitals are only approximations of reality. They're good approximations, but approximations nonetheless, because we can't solve problems with more than one electron exactly. Note that some wavefunctions also give very unclassical locations and properties for electrons; for example, there is the phenomenon of tunnelling, whereby an electron can be on the other side of an energetic potential barrier even though it shouldn't have had enough energy to make it there. Sort of like you being able to drive a car over a hill with no gas in the tank.
But that's getting a bit far afield of the topic at hand.
Quote:
So "combining" atoms to form molecules changes the probability distribution of the orbitals (and adds more "valid" orbitals, since it's only quantized states).
Essentially, yes.
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
dimis
Responsible
Supreme Hero
Digitally signed by FoG
|
|
posted November 06, 2009 02:22 AM |
|
|
I probably need to re-read some parts to make them clearer, but so far ... thanks!
____________
The empty set
|
|
ohforfsake
Promising
Legendary Hero
Initiate
|
|
posted November 08, 2009 04:24 PM |
|
|
|
I had the opportunity to read some more, I'm impressed by your dedication and the information you present, I don't really have much to comment right now though, but thanks a lot.
|
| |
|
|
