| The Science of Small |  This thread is pages long: 1 2 3 4 · «PREV This thread is pages long: 1 2 3 4 · «PREV |
|
Warmonger

  
     
Promising
Legendary Hero
fallen artist
|
 posted November 08, 2009 04:28 PM
posted November 08, 2009 04:28 PM |
|
|
OMG, it's just what drives me mad this semester and what I need to learn today  Begone, perish! Begone, perish!
|
|
Corribus


Hero of Order
The Abyss Staring Back at You
|
 posted November 09, 2009 05:50 PM
posted November 09, 2009 05:50 PM |
|
Edited by Corribus at 17:53, 09 Nov 2009.
|
Quantum Dots, Part 2:
I don’t think any introduction is really required at this point, so I will continue basically where I left off, with semiconductors.
Excitons
When a photon hits an electron which is in a molecule, and the energy of the photon is equal to the amount of energy between the state in which the electron is currently located and some other unoccupied state, the electron absorbs the photon (and its energy), causing a transition between states. This is known as the Bohr condition. There are some other requirements as well, but we can ignore them.
This happens to electrons in semiconductors, too, and it shouldn’t be surprising that electrons absorbing photons with energies larger than the band-gap energy are easily promoted from the valence band into the conduction band, because of the near-continuum of empty states there. When an electron is excited into a vacant space in the conducting band, the electron leaves behind an “open space” in the valence band, a partially empty orbital which physicists refer to as a “hole”. Because the valence band can almost be thought of as a static continuum of electrons, this hole behaves very much like an electron of positive charge. In other words, the hole is treated as a particle, and therefore an electronic absorption results in the “formation” of two particles of opposite charge: a negatively charged electron in the conduction band and a positively charged hole in the valence band.
Once such an excitation occurs, one of two things can happen. The first possibility is that the two particles can go on their merry way, the electron in one direction and the hole in another. If you are clever, you can engineer it so that you can gather electrons at one end of your material and holes at the other, creating a unidirectional flow of electrons/holes that is also known as an electrical current. Essentially what you would have is light driving the flow of electrons in a semiconductor, AKA this:

Anyway, the other thing that can happen is the formation of an exciton. Because you essentially have a negatively charged particle in close proximity to a positively charged particle, the two can trap each other and form something that looks very much like a hydrogen atom. This metastable dual-particle system is known as an exciton. This exciton can itself move around (migrate) or, after some amount of time, the electron will spontaneously recombine with the hole (it’s an empty space, after all), emitting a little bit of light in the process. The color of the light is usually a little bit less than the material’s band-gap energy, and because most semiconductors have band-gaps in the visible region of the electromagnetic spectrum, the bit of light is usually colored. (Excitons can also combine without emitting light, but that’s no fun, so let’s pretend it doesn’t happen.)
Here’s a little diagram illustrating these possibilities.
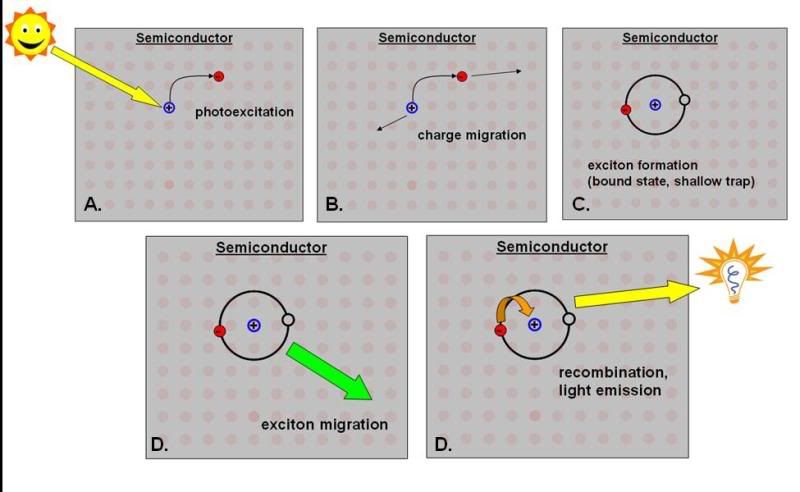
Figure caption: Figure demonstrating some light-driven processes in a semiconductor. In (A), photons from an ambient light source are absorbed by an electron. The electron (red) is excited into the conducting band, leaving behind a hole (blue). (B) The electron and hole can move independently of each other (charge migration). If many excitations happen and electrons can be made to flow in one direction, and holes in another, the material can be the basis of a solar cell. (C) Alternatively, the electron and hole can entrap each other, forming a hydrogenic bound state known as an exciton. (D) The exciton may itself migrate through the material or (E) the electron and hole can recombine, in many cases emitting a photon. Photons emitted by excitons in an ideal material are nearly monochromatic.
Aside: if you purposely inject electrons and holes into opposite ends of a semiconducting material using a battery, they will migrate through the material (as in B), until they meet and in many cases form an exciton. These electro-generated excitons will recombine to emit photons (as in D). This is the basis for the operation of the light emitting diode (LED), AKA

You should be able to guess that to make different color LEDs, you just change the semiconducting material. Since different semiconductors have different band-gaps, the emission energy (color) of formed excitons are also different. Traditional LEDs were made with inorganic semiconductors like zinc selenide. Now LEDs are more and more often being made with organic semiconductors, like conducting polymers (PLEDs), which have the advantage of being highly processable, opening up opportunities in flexible display technologies.
Ok, where was I? Oh right.
Confinement
Let’s go back to the hydrogen atom for a moment.

As I’ve discussed earlier, when in its lowest energy state, the electron orbiting the hydrogen nucleus (a proton) has a roughly spherically symmetric probability distribution. That is, for a given distance from the nucleus, the electron has an equal probability of being found in any direction from the nucleus. The most likely distance at which the electron can be found is known as the Bohr radius, which is equal to about 0.05 nm. In a classical model, this distance would be determined by the opposition of centripetal and Coulombic (electrostatic) forces.
An exciton, as I’ve said, is like a metastable hydrogen atom. It has orbitals and states just like a hydrogen atom. And, like a hydrogen atom, it also has a Bohr radius (known here as the exciton-Bohr radius, alpha) which is the most likely distance the electron will be away from the hole. This distance is usually quite a bit larger than that of a hydrogen atom, because the exciton is not formed over “free space”. That is, there are other electrons and such in the background that change the electrostatic forces which determine what the “optimal distance” is.
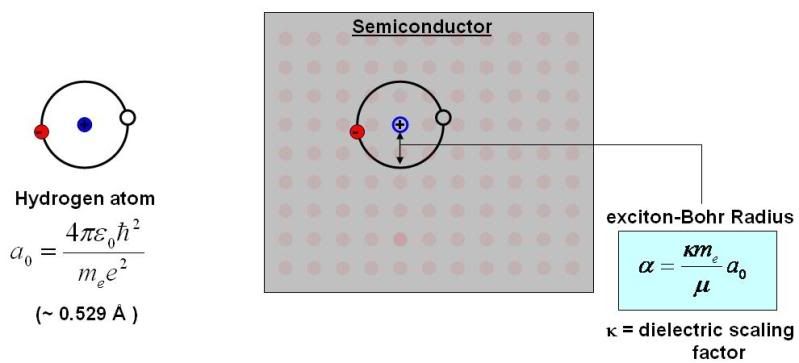
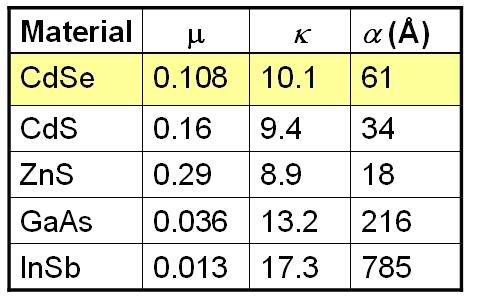
Basically, the exciton-Bohr radius is scaled by a constant known as the dielectric scaling factor, kappa. Kappa is just a numerical value which depends on the material. Some are listed below for a few semiconductors that are popular materials for quantum dots. Notice anything special about the alpha values? That’s right, they’re all on the order of a few nanometers. So are the diameters of most quantum dots. Coincidence? I think not!
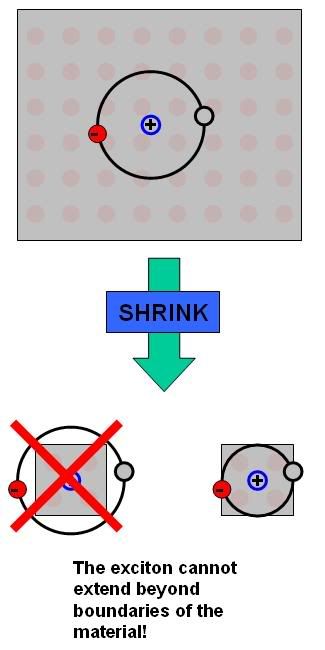
Alright, so here we are. The thing is that in a bulk material, when an exciton is formed the electron can happily reside at its most optimal position away from the hole (the exciton-Bohr radius). Such an exciton is a “classical” hydrogenic system very similar to those of a conventional hydrogen atom, with a radius scaled only by the dielectric scaling factor for the particular material. However, what happens when you shrink the size of the material down so that the chunk of semiconductor is on the scale of, or smaller than, the exciton-Bohr radius? As you might imagine, there is a huge potential energy barrier at the edge of a material. Which basically means that, while it’s not mathematically forbidden, the electron doesn’t like to exist outside of the material. The edge of the material is a boundary of sorts, and so when you shrink the size of the material down to about the scale of the exciton-Bohr radius, you start to squish the electron closer to the nucleus than it really wants to go, a phenomenon we call quantum confinement.
A Particle in a Box
What does quantum confinement do?
Well, let’s look at one simple model. One of the first problems students solve in introductory quantum mechanics classes is called the “Particle in a Box”. It’s a very easy problem with a simple mathematical solution that nonetheless demonstrates a lot of important principles about quantum mechanics. In this problem, we confine a particle (electron, say) into a region (the box) that has absolutely zero potential energy inside the box but infinite potential at the boundaries of the box. Translated: there’s no reason for the electron to energetically favor any position inside the box over any other position inside the box, but it absolutely cannot be outside the box. We then ask the question: if we were to peak inside the box at any particular time, where is the particle likely to be and what are its properties?
It’s not necessary to go through the math but let’s just take a look at the solution. As in the case of atoms/molecules, we find that the electron/particle is only allowed to have certain energy values, and its probabilistic position is defined by orbitals, although in non-electronic non-molecular systems we usually just call them wave-functions. In the figure below, left side, I have plotted out the allowed states (each described by a “quantum number”, n) in different colors (and their associated wavefunctions – dotted lines) as a function of energy (y-axis) for boxes of three different arbitrary lengths (L, 1.5x L and 2x L). The x-axis in each plot is position. [Just FYI, the amplitude of the square of the wavefunction value at position x is proportional to the probability of finding the particle at position x. So, for instance, in the n = 1 state, the most probable position for the electron is the center of the box, where the wavefunction has the largest amplitude.] What should be immediately apparent is that as the box size (L) is increased, the allowed energy levels get closer together. You can extrapolate this to a box of infinite size (a classical limit – particles can be anywhere), and you’ll see that in that case the particle can take on practically any energy value, just like a classical object would.
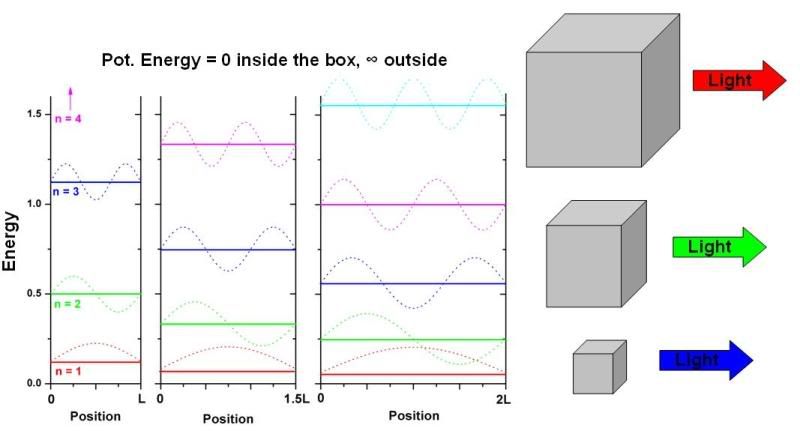
The important point is that because energy levels get closer together as the box size increases, this means that light emitted from an excited electron in a big box is lower energy – or more red colored – than an excited electron in a small box, as illustrated in the above figure.
The excitons in quantum dots can be, to a really crude approximation, treated like particles in boxes. As the size of the quantum dot becomes smaller than the “ideal” exciton radius, the exciton is confined to a smaller and smaller area, which results in the gaps between allowed energy states increasing in energy, and the emission color shifting to higher energies (more blue). Because you can easily control the size of semiconducting particles through synthesis, you can obtain virtually any color of emission that you want. And different materials give rise to different color ranges, as the following figure shows (left side, actual emission from QDs of different sizes; right size, emission spectra (number of photons as a function of wavelength/energy) for various QDs made from different materials.
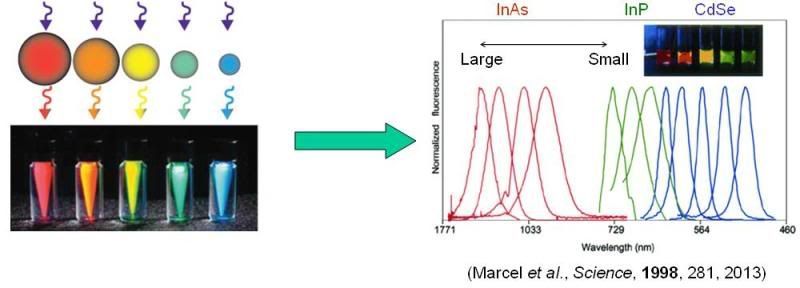
The particle in a box model is an admittedly crude model that doesn’t quantitatively fit real data very well. For one thing, quantum dots aren’t cubes; for another, the background potential isn’t zero. Also, you can get different effects by changing the shapes of the dots from (roughly) spheres, to elongated rods, or pyramids, or whatever. Nevertheless, the PB model still explains the trends: smaller dots, bluer color and larger dots, redder color. The latter is limited, obviously, by the band-gap in the bulk material. Once the QD becomes big enough that you’re no longer “squishing” the exciton, that’s about as far as you can red-shift the fluorescence (PL) properties because at that point, the electron is in its "optimal" orbit position.

Blinking
Well that’s about it for how QDs work. However, before discussing what these suckers can be used for, I wanted to mention one more aspect about QDs that is important, and that’s blinking.
When it finally became possible to observe single molecules and particles using powerful microscopes, it was found, to everyone’s surprise, that when excited by a continuous laser, many molecules and particles flicker. The technical term for it is “fluorescence intermittency”. The jargon is “blinking”. Below is a little animation of blinking of a common conducting polymer called MEH-PPV (yeah, it happens in organic molecules, too), and below that are plots of fluorescence intensity as a function of time for two CdSe quantum dots. The blinking behavior is pretty apparent I think.

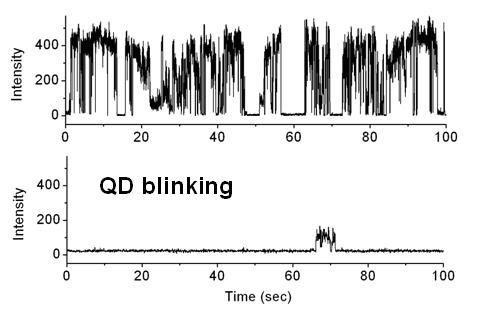
To be honest, blinking is still not completely understood and a lot of people still do a lot of research on it, not only to understand what causes it, but also to find ways to prevent it. After all, if your molecules are spending half their time in a dark state, that reduces their usefulness in applications where brightness is important, like in biomedical imaging. You should see some of the papers out there that try to model that statistics of on and off times. :shudder:.
Anyway, most proposed mechanisms, at least for quantum dots, boil down to some sort of surface chemistry. Remember all the way back a few pages ago when I talked about surface area and changes in chemistry? Well, QDs have so much available surface area that it is inevitable that oxygen or other reactive chemicals will react with atoms on the QD surface. These reactions cause changes to occur in the photophysical properties of the QDs (shifts in color over time, for example), but also can cause intermittent quenching of excitons so that they relax by other channels than fluorescence. I don’t really want to get too much into it except to show you a popular solution to the problem, and that is to coat the QDs with a really thin secondary semiconducting layer. The coating basically protects the QD from surface reactions, as you can see below for cadmium selenide (CdSe) QDs coated with a layer of zinc sulfide (ZnS) - the core-shell dots are much brighter than the uncoated ones:

Core-shell QDs are used ubiquitously nowadays because they are so much brighter than vanilla dots. You’ll see them show up a lot in all of the applications I’ll highlight in the next article.
Conclusions
Well at this point you should have a pretty good basic understanding of how QDs work, which are in my opinion nanotechnology’s most fascinating posterchildren. But more than that, you should have a sense of how materials at the nanoscale manifest changes in properties that you wouldn’t necessary predict from classical physics. Hopefully you have a sense of why quantum physics is important to the study of nanomaterials. In the final part of this article, I’ll highlight five important technological applications of quantum dots that will affect your life, from electronics to medicine to food.
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
winterfate

 
    
Supreme Hero
Water-marked Champion!
|
 posted November 10, 2009 12:40 AM
posted November 10, 2009 12:40 AM |
|
|
Shiny!
The complexity of this subject makes me glad I'm not studying Physics as my Major. 
____________
If you supposedly care about someone, then don't push them out of your life. Acting like you're not doing it doesn't exempt you from what I just said. - Winterfate
|
|
Corribus


Hero of Order
The Abyss Staring Back at You
|
 posted November 10, 2009 03:56 AM
posted November 10, 2009 03:56 AM |
|
|
LOL, biology is just as complex. It's just not as.. hmm, wacky. 
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
Warmonger

  
     
Promising
Legendary Hero
fallen artist
|
 posted November 10, 2009 07:43 AM
posted November 10, 2009 07:43 AM |
|
|
Complexity? These are only some stories. There's advanced mathematics behind it all to start with. Corribus did not ask you to integrate Schroedinger's equation 
|
|
ohforfsake

  
     
Promising
Legendary Hero
Initiate
|
 posted November 15, 2009 07:15 PM
posted November 15, 2009 07:15 PM |
|
|
Very interesting, I'm looking forward to the next article. 
Also, though it may be because I lost something somewhere, but you started to use the shortening "(PL)", in this part:
Quote:
Once the QD becomes big enough that you’re no longer “squishing” the exciton, that’s about as far as you can red-shift the fluorescence (PL) properties because at that point, the electron is in its "optimal" orbit position.
Which, if I understand it correct is the limit of where QD looses their "function", as you get to a "normal" state, but what does PL exactly stand for, it'd be nice to know, given you use the term later on, and expect it to be known already. 
|
|
Corribus


Hero of Order
The Abyss Staring Back at You
|
 posted November 15, 2009 11:20 PM
posted November 15, 2009 11:20 PM |
|
Edited by Corribus at 23:21, 15 Nov 2009.
|
I'm sorry: PL is an abbreviation for photoluminescence. Such as, in this case, fluorescence. Not all fluorescence is photoluminescence, though - fluorescence from LEDs, for example, is a form of electroluminescence (EL). Confused yet? 
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
ohforfsake

  
     
Promising
Legendary Hero
Initiate
|
 posted November 16, 2009 12:38 PM
posted November 16, 2009 12:38 PM |
|
|
Okay, I see, thanks for explaining. 
|
|
Corribus


Hero of Order
The Abyss Staring Back at You
|
 posted December 10, 2009 03:22 AM
posted December 10, 2009 03:22 AM |
|
Edited by Corribus at 05:42, 10 Dec 2009.
|
Apologies for the delay. This section took a considerable amount of time to research and write, particularly since I only have an hour or so after work each day to dedicate to such endeavors.
Quantum Dots, Part 3: Applications.
The following gives descriptions of some major applications of QDs. Because the number of papers published in these areas is virtually endless, particularly in the biomedical fields, in some cases I have simply chosen a specific paper or two as a representative example of the application being discussed. Due to the length of some of these mini-articles, I won’t post them all at one time. Rather, I’ll post them as individual posts to keep it manageable. Here are the applications I'll briefly talk about.
Anticounterfeiting
Bioimaging: imaging of live cells
Biosensing: detection of individual pieces of DNA
Bioimaging: imaging cellular processes with single QDs
Nonbiological sensing of gasses and toxins
White light LEDs
Lasers
Quantum Computers
Quantum Dots in Anticounterfeiting
We like to call hellfire down upon “greedy pharmaceutical companies”, but at least when you purchase a drug from Pfizer, you can be reasonably confident that the drug is manufactured in a well-controlled environment in accordance with a thousand-page list of US Federal government regulations. Pfizer’s laboratories are routinely inspected; their drugs are routinely screened for impurities, efficacy, safety, etc. For that peace-of-mind, they also charge a lot for their products. Abdul’s Drug Emporium, based in India, isn’t subject to all those regulations, and because Abdul’s drugs are manufactured in a rat-infested plant which is operated by workers who don’t wash their hands, and Abdul doesn’t have to purchase any of that fancy equipment to assess the purity or efficacy of his products, Abdul can sell his drugs for a few percent of what Pfizer does. So you might understand why an online website like www.cheapdrugs4u.com might, say, want to purchase their drugs from Abdul’s wholesale, put his drugs in distinctly Pfizer-like bottles, slap cleverly-made Pfizer-like labels on them, and sell such drugs to you, the unwary consumer, at Pfizer-like prices. Big profit for www.cheapdrugs4u.com (not a real site!). Small benefit to you when you get chronic lead poisoning from Abdul’s adulterated product - especially when you thought you were getting something from Pfizer.
Anticounterfeiting measures exist not only to protect Pfizer’s property rights, but also the consumer’s rights and, indeed, safety. This is true not only for the drug industry, but also the food industry, and indeed any industry which has an interest in preventing people from making counterfeit versions of its products. Traditionally, barcodes have been used to uniquely identify commercial products, but sophisticated thieves can easily put fake barcodes on their counterfeited products – even clever shoplifters can print their own barcodes these days. Barcodes also take up a lot of packaging space, which costs money and also makes the labeling of small products (such as individual pills or individual lemons) problematic, and barcodes also have to be properly oriented in order to be read, which introduces an annoying bottleneck at both the production facility as well as the checkout counter. So what’s an honest company to do?
Quantum dots to the rescue!
Let’s review: two of the biggest advantages of quantum dots over conventional (molecular) fluorescent dyes is (1) their emission wavelengths can be tuned with a high degree of precision and (2) they have remarkable color purity. As a result, mixtures of quantum dots of varying colors (sizes) can be used to formulate “digital counterfeiting inks” which, when scanned, can uniquely identify a product. By fine-tuning the number and emission wavelengths of the quantum dots in the ink, one can create a digital fluorescence code unique to the ink: the number of codes increases exponentially when multiple wavelengths and multiple intensities are used at the same time. In general, n intensity levels with m colors generate (n^m - 1) unique codes, although in practice the number of functional codes is somewhat lower. The technology works by reading out the digital codes after illumination of the ink with UV light. QD fluorescence is analyzed, which reveals the authenticity/identity of the item.
Caption: Calculations suggest that the use of six different wavelengths and ten intensity values could create one million distinct codes. This image shows how three different quantum dots can produce 24 unique codes.Source.
The real advantage here, is, of course, that the technology, while simply to use, is sophisticated enough that it can make counterfeiting the inks very difficult. Not only is QD manufacture not very simple for amateurs without well-supplied chemistry labs, but the would-be-counterfeiter would have to know a lot of precise information about the ink in order to copy the code exactly, making counterfeiting almost impossible.

Source.
Here’s just a fun fact to drive home the importance of this technology: according to a press release from Life Technologies, Inc. “The worldwide counterfeit goods trade, excluding counterfeit money, is believed to be on the order of $1 trillion annually. The U.N. estimates counterfeit drug sales alone were over $300 billion in 2008, while the World Customs Organization believes that other counterfeit goods sold for more than $600 billion. According to U.S. Immigration and Customs Enforcement, these losses cost American industry and trade between $200 billion and $250 billion each year and equate to 750,000 American jobs lost.” So you can see that new methods to prevent counterfeiting of consumer goods would be a big deal. (Source.
Sample of quantum-dot inks from Evident Technologies:

Source.
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
winterfate

 
    
Supreme Hero
Water-marked Champion!
|
 posted December 10, 2009 05:53 AM
posted December 10, 2009 05:53 AM |
|
|
*peeks into forum*
You updated! 
Yep, I've been lurking for a long while. Too busy to do much more, but thankfully my classes will be over soon, and my last final should be before Christmas. 
Anyways:
@Corribus: Insightful as always. I have to do a presentation for Industrial Microbiology (on Tuesday) related to Nanotechnology's applications in Biotechnology. Interesting that you posted this precisely today. 
____________
If you supposedly care about someone, then don't push them out of your life. Acting like you're not doing it doesn't exempt you from what I just said. - Winterfate
|
|
Corribus


Hero of Order
The Abyss Staring Back at You
|
 posted December 10, 2009 03:36 PM
posted December 10, 2009 03:36 PM |
|
|
@Fate
Well, the next section(s) on bioimaging should be useful to you, then.
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
|
ohforfsake

  
     
Promising
Legendary Hero
Initiate
|
 posted March 24, 2010 07:57 PM
posted March 24, 2010 07:57 PM |
|
|
I never noticed the december update in this thread before, I'll read it in a moment. Meanwhile, I came back to this thread, because I saw this link: - http://io9.com/5497720/first-quantum-effects-seen-in-visible-object
I understand the link, as saying as an effect of the quantum world have been produced in the macroscopic world (in that case, screw you mvass, you, and your forceful seperation of macro-world and micro-world  ), which seems rather amazing, and I suppose it'd belong here. ), which seems rather amazing, and I suppose it'd belong here.
____________
Living time backwards
|
|
Corribus


Hero of Order
The Abyss Staring Back at You
|
 posted March 25, 2010 03:48 PM
posted March 25, 2010 03:48 PM |
|
Edited by Corribus at 15:50, 25 Mar 2010.
|
Well part of the reason we don't perceive quantum effects in the macro world is buried in the mathematics. There's often inverse (exponential!)proportionality between quantum effects and mass, and quantum effects are also usually scaled by Plank's constant, which is an extremely small number. Quantum tunnelling, for instance, is only significant for particles lighter than (roughly) a proton. While an oxygen atom obviously is a "quantum thing", even for this "heavy" object, the probability of oxygen tunnelling is almost insignificant. Now imagine what the probability of quantum tunnelling of a moving tennis ball would be. We could calculate it if we wanted to, but the probability would be so low (think 10^-XX, XX being a very large number) as to be almost ridiculous. Likewise, a 1 kg loaf of bread flying at a modest 10 m/s technically does have a wavelength, but it is ~6.6 to the power of minus 35 meters! I can't even begin to describe how tiny of a length that is, and it is certainly well beyond anything we could measure, perhaps beyond anything that is actualy measurable. So, in some sense, it should be no surprise that we cannot observe quantum effects in classical systems. That doesn't mean they aren't there. It just means they are practically unmeasurable (and not useful, as well).
Aside from the mathematical argument of scale, there's the one of incompleteness. Even if we could measure a length scale on the order of 1 to the power of -35 meters, that value was calculated under the assumption that quantum mechanical equations are applicable to macro-scale objects. For de Broglie wavelengths, maybe that assumption is justified; for other QM ideas such as, say, superposition, it is not so clear. It has been speculated (by Sir Roger Penrose, to name one) that the successful incorporation of gravity and relativity into QM theory will clarify the seeming incompatibility between quantum and macro physics. I.e., gravitational effects cause wavefunction collapse. Some of the experiments proposed to study the relationship between gravity and quantum particles are rather mindboggling, involving enormous (planet-sized) interferometers made from orbiting satellites.
In any case, the article you linked to is interesting, and I did download the research article published in Nature. I haven't read it yet. When I do, if I have anything else to add to the article you linked to, I'll post it here.
____________
I'm sick of following my dreams. I'm just going to ask them where they're goin', and hook up with them later. -Mitch Hedberg
|
| |
|
|





